研究逻辑的目标是评价自然语言

目录结构:

第一部分：逻辑与语言
- A.推理
  - 逻辑学概念
  - 论证的分析
- B.非形式逻辑
  - 语言的定义
  - 谬误
第二部分：演绎
- 古典逻辑
- 现代逻辑
第三部分：归纳
- 类比与因果
  - 类比推理
  - 因果推理
- 科学与概率
  - 科学和假说
  - 概率

逻辑学导论

基本概念

我们通常依赖于习惯来做出或者接受一些断言，如果旨在做出可靠的判断，最坚实的基础就是可靠的推理。

命题（proposition）

命题是推理的基础，如果一个问题没有断定（assert）任何东西，所以不是命题。与命题不一样，问题，命令和感叹都是非真非假。

命题是由语言给出的，但命题却不依赖于任何语言。命题通常指人们用陈述句所断定的东西。

复合命题 即在一个命题中包含了别的命题

合取命题：分别肯定其所有分支命题
析取命题：命题的任何分支都没有得到断定
假言命题：“如果-那么”的命题

论证

推论在其他命题的基础上断定另一种命题，是将一组命题结合起来的过程，这样的一个命题簇就是论证。任何单个的命题都无法构成论证，论证是由一组命题构成的。用前提和结论来描述这种结构。

推论：在其他命题的基础上断定另一种命题，是将一组命题结合起来的过程。
论证：一个命题从其他命题推出，后者给前者之为真提供支持。任何单个的命题都无法构成论证，论证是由一组命题构成的。
- 前提：即被肯定或假定为接受结论的根据或理由的命题
- 结论：以论证中的其他命题为根据所得出的那个命题

单个命题无法构成一个论证
假言命题看起来像一个论证，容易混淆。
祈使句（命令句）不能成为一个命题，同样它也不能作为一个结论。
反问句（诘问句）可以作为命题。通常作为躲避争论的一种聪明策略。
隐含命题：论证中存在着一个或更多构成命题未被明确陈述但又假设能被人理解。一个省略式的前提也许得不到普遍认可，一个论证者也许故意不将关键的前提陈述出来，从而免于它被攻击。

💡Tip : 假言命题看起来像一个论证，容易混淆。例如 “如果我不喜欢人和蔼可亲，那么我就省去了喜欢他们的麻烦。” 这个命题的两部分都没有得到断言。“我不喜欢人和蔼可亲，那么我就省去了喜欢他们的麻烦。” 这句话却有一个论证。第一个命题作为前提被断定，第二个命题作为由前提推到而出的结论被断定。

语句的重塑能够起到澄清论证和构成命题的作用。

许多语段看起来像是论证，实际上是说明。例如： “它叫巴别塔是因为耶和华在那里变乱天下人的言语” 对于这种 Q 是因为 P 在 Q 已知为真的情况下，我们不必提供理由来支持它为真，这时候 P是对Q的说明。有时候要区分作者的意图是说明某事实还是要为该说明中的关键命题做论证，并不容易。如何断定 “Q因为P”是说明还是论证，要看Q在该语境中的身份是什么，如果Q是一个其真实性需要建立或确证的命题，那么 P 就是其为真的前提，若Q是一个已知其为真，至少在这个语境中没有疑问的命题，那么P就是为什么Q成为真命题的阐释，这样 Q 因为 P 就是一个说明。

演绎论证和归纳论证

演绎论证均断言前提对结论的决定性的支持。归纳论证则没有这种断言。

归纳论证：结论从归纳而来；其结论是或然的

演绎论证：结论从推导而来；其结论是必然的

演绎论证的有效性：即如果前提为证，则其结论必定是真的，则这个演绎论证是有效论证。因为归纳论证永远达不到逻辑的必然，所有有效性不适用于归纳论证, 有效性也不能适用于单一命题本身。有效性、无效性是论证的属性。 论证的有效性不能保证其结论的真实性.

一个论证是有效的，并且其前提都是真，我们就可以断定其结论也是真的。 我们称之为可靠的论证。

论证的分析

解析（paraphrase）法：即用清楚的语言和逻辑顺序表明论证中的命题。

图示法：首先给论证的每一个命题逐次赋予一个置于圆圈中的数字，在数字间用箭头符号展示其中的前提与结果的逻辑关联，这样就可以不用重述前提就构建出表明前提和结论之间关系的图示，结论总是出现在支持它的前提的下方。同等级的前提在图上的同一行列出。垂直的花括号表示论证的前提只有结合在一起的时候才能给予结论支持

当一个论证含有未明确陈述出来的隐含前提时，解析法允许我们直接把隐含前提列出来。而图示法则既需要列出隐含前提又要以某种直观形式表明它是被附加到原来论说之上的，如括号。

当一段话中有两个结论时，图示法更有效。又或者一段话中出现两个或更多的论证，或一个论证有两个或更多的前提。

复杂的论证可能是由几个论证多重复合而成，有些命题只作为前提，有些命题即作为前提又作为分结论，还有一些命题通过不同的语词被多次重复。

推理是从已知的前提推出结论的过程。用于决定自己应如何行动，评价他人的活动，为道德或政治信念进行辩护等方面, 构建好的论证以及评价一个论证的技能有巨大的价值。（平时可以做一些逻辑推理题目）

回溯分析是企图说明事情为何从过去的状况发展到现在的状况的推理。

非形式逻辑

语言的功能：带 * 为主要功能

* 表达性：“真棒”、“执子之手与子偕老”；
* 指令性：小心驾驶、“请出去”
* 信息性：前方有障碍。
情感性：父母对孩子说 “这种行为非常恶心”，表达了一种态度。
礼节性：“你好”
述行性：“我为自己的愚蠢言辞道歉”，“祝贺你……”、“我答应你……”

进行推理——断言或否定某命题，形成或评价论证等等。我们主要关心的时语言的信息性。

语言的用法与形式的区别：语言的不同用法时通过不同形式达到的。

句子的形式：

陈述句：进行推理的时候，所使用的一般是陈述句。
感叹句：一般用来表达情感
祈使句：常用于指导行为。
疑问句：

由于自然语言的模糊性与其用法的多变性，语言的功能与特定的语法形式难以总是对应，例如：疑问句也能表达情感：“你什么意思？” 陈述句形式报告一个事实也能起到指令功能：“天哪，要迟到了。”，
语段的语法形式和作者想要的用法之间没有必然的联系，任何用法的语言可能以任何语法形式出现。
因此，要确定一个句子的真正功能，语境就再次起到了至关重要的作用。。

在信息模式中,我们区分一个句子所构成的事实和关于说话者的事实，就某人自己观点的一种陈述与其展开论证绝不是欺骗性的。

情感语言

一个给定的句子或段落可以有多种功能，例如报告事实的同时可以表达感受。聪明地使用语言可以使其具欺骗性，不慎使用则可能会导致不必要的误解和论争。我们用来传达信念的语词可能是中立和精确的，但是它们却有可能影响听者的情绪。通常由于某些语词引起的负面态度导致了委婉语的出现以及委婉语相应的传统语词代替。
（对女人说话时要着重考虑其语言的情感方面）

委婉语：即用温和的词汇表达冷峻的现实。

逻辑上，我们追求的是尽可能没有被情感意义所扭曲的语言。

广告行业中，玩弄听众和读者的情感是一种核心技巧。劝服和推销的时候，操纵态度变成了一种专业技巧。

政治宣传中其修辞技巧应用非常普遍，防御诡计的最好方法就是理清楚我们语言真正的用法，防备那些用语言颠倒黑白的人。

争论

争论可能源自于双方对待同一事实的不同信念，也可能是因为双方对相同事实的不同态度。这种不确定性及其可能带来的混淆可能因为论争中所使用语言有大相径庭的情感意义而起。

信念歧见：两个人可能会在某事情是否已经实际地发生上意见相左。

a.革命是一种固有权利。当人民被政府压迫时，如果他们足够强大，那么通过或者从政府那里收回权利，或者推翻它，并更换一个比较可接受的政府，将自己从压迫中解放出来，这是他们的天然权利。——Ulysses S.Grant,Personal Memoirs,vol.1

b.煽动革命是叛逆，不但反人类而且反上帝。-Pope Leo XIII,Immortale Dei,1885

信念歧见可以通过确认事实而得到最好的解决。为了明确这些事实，如果它足够重要，可以询问证人、查阅文本和检查记录等等。当事实得到了确认、解决了事实问题时，歧见就会得到解决。科学的探究方法在这里都可以用到，这将足以指导他们直面有关信念歧见的事实问题。

态度歧见: 对事情的感受不同

a.今天，人们对美国政府感觉如何呢？我回答说，与它联系在一起，让人们感到蒙羞。——Henry David Thoreau, An Essay on CivilDisobedience,1849

b.我们（美国）现有政府即使有所有这些缺点，它仍是无与伦比的最好的政府，或者迄今为止存在过的最好政府。——Thomas Jefferson

如果以确证事件发生与否为目的，对解决这样的争论不会有什么效果，因为争论的问题并不是事实，这种歧见不是关于事实是什么而是关于怎样评价它们的对立。修辞艺术也可能富有成效（当然，它在解决事实问题上完全没有价值）。

要解决既有事实方面又有情感方面的论争，非常重要的一点即明确双方争论的真正问题所在。

简单通过确认论争的本质并不能使我们达成一致。但是只有在确认了论争的真正本质，明确了论争双方所用语言的不同功能之后才有可能解决歧见。

言辞之争

许多争论都是实质争论（无论是关于信念还是关于态度的），还有些争论是纯粹的言辞之争，其源于语言的误解。争论中所使用的词语有多个意思（含混的）但这种含混性没有却没有被争论的双方发现。

纯粹的言辞之争中并不存在实质的歧见。

应对：要揭示和解决言辞之争，需要辨识出这种含混性，区别和澄清争论中关键词项的不同含义。

实质争论

不管是事实还是信念歧见、态度歧见引起的争论，都是实质争论

表面是言辞的但实际上是实质的争论

这种争论更为复杂。其中有言辞的误解，也存在着超出语词含义的歧见。

总之：如果在交流中面对一个论证，我们首先追问其中是否存在可以通过澄清多种意义而消除的含混性。如果有。我们必须追问是否清除掉这个语言上的问题就能解决该争论。如果能解决，该争论就是纯粹言辞上的。如果不能解决，则我们面对的是一个以纯粹言辞争论面貌出现的实质争论。

定义

定义对于消除言辞之争非常有帮助。定义总是对符号的定义，只有符号具有定义能够说明的意义。

我们有时候会说某事物得到了定义，这是误导人的，事实上，我们定义的总是符号。

我们可以给“椅子”这个词下定义，因为它有意义。但我们不能定义椅子本身。我们可以坐在椅子上，或者烧掉它，或者描述它，但是我们不能定义它，因为椅子不是一个具有意义从而需要说明的符号。

被定义项（definiendum）：指被定义的符号
定义项（definiens）：定义项是对被定义项的定义。

定义种类

规定定义：规定定义被定义项再引进之前没有意义。指将意义指派给某个符号的定义。有时也成为名义(nominal)定义，它的定义被视为一种请求或指令，因此它是指令性的而不是信息性的，指令可能被拒绝，但是它们非真也非假。但是规定定义可以被评价为有用或无用。规定定义能够减少语言的情感角色和简化对话，规定定义有利于防止无谓的冲突。
词典定义：词典定义被定义项再引进之前具有一个先在的和独立的意义。被定义的词项一般都有某种固定的用法，如果定义的目的是为了解释这种用法或消除歧义，那么该定义就是词典定义。词典定义或真或假，例如给鸟添加定义项是“哺乳动物”，那么该定义显然为假。
精确定义: 用来消除语词的歧义和模糊性。被定义项不是新词语，其用法虽然模糊但已经固定下来。因此不能自由的选择意义而指派给被定义项，必须尽可能的保持固定用法，使已为人知的词项更加精确。为了解决被定义项的模糊性，事实上可能完全是规定定义的问题。例如法律的定义必须是精确的。
理论定义：科学上关于定理和理论的定义，例如行星的定义，柏拉图寻找“正义”的定义，斯诺宾莎试图定义“束缚”和“自由”。比如还有“权利”，“民主”的定义都需要理论定义，
说服定义：上述四种定义主要关注语言的信息性。有些通过影响态度或激发情感以解决争论，我们将之称为说服定义(persuasive definition). 情感色彩可以被偷偷注入一个定义语言里，而这个定义却伪称准确并表面上显得客观。正如我们需求区分好与坏的推理一样，我们必须警惕被说服定义所愚弄

判断一种定义具有哪种或哪几种功能时，就像在语言的其他地方一样，语境在此的表现也很关键。

外延和内涵

定义表名一个词项的意义（meaning），对定义的理解不仅能通过其用法，还能通过的结构达到。

普遍词项：可以运用于多个对象的类（class）的词项。

外延性意义：行星是一个普遍词项，可以适用于水星，木星，火星等同等含义，词项行星意味着所有这些对象的即可，而所有行星的汇集（collection）就构成行星的意义，即其外延性意义, 一个普遍词项的外延（又称指谓 denotation）意义是构成该词项外延的对象的汇集。

内涵意义：其外延内所有对象的共有属性，如果我们知道这些属性，就知道了这个词项的意义而无需知道其外延，意义设定了词项外延的标准，这些属性称之为内涵意义（connotative meaning）。即普遍词项指谓的所有对象并且仅仅那些对象共同拥有的属性集，称作那个词项的内涵（intension 或 connotation）

词项的内涵决定外延。外延不决定内涵。词项可以具有不同的内涵但外延相同，而具有不同外延的词项却不可能有同样的内涵。

给一个词项添加性质时，我们就说内涵增加了，然而增加内涵也就减少了它们的外延。但并不总是这样，增加有些内涵不会导致其外延的变化，也就是说，如果外延变化，那么它将是沿着内涵的反向变化例如 “人” 加上 “中国人”，加上“女人”。每加一个性质，内涵都随之增加。

有些词项的外延是空的，例如龙，龙是一种巨大的、拥有蛇、鹰、牛、鹿等动物特征的神话生物，它就没有外延。

外延定义

指出被定义术语的外延。该方法非常有效，但却十分局限。

三种外延定义

列举定义：通过对一类事物的部分列举，普遍词项的意义仍然非常不确定。
实指定义：指着被定义对象来定义。实指定义无法定义不指谓任何东西的词，当我们说不存在的独角兽时。独角兽这个词没有所指。
准实指定义：定义种姿势或手指的指示伴有一些其意义被认为已为人知的短语

内涵定义

主观内涵：对于说话者来说，就是他认为该词指谓对象所具有的属性集。主观内涵无法达到定义的目的。
客观内涵：是词项外延的所有对象共同拥有的属性全集，由于没有人能够全知，所以客观内涵无法被人所知晓。
规约内涵：对任何对象来说，决定其是否是某词项外延的一部分时，我们都统一使用同样的标准。内涵通常用来指规约内涵。
- 词项的规约内涵不必是它所指谓事物的内部特征，它可能和这件事物的起源或根其他事物有关。如“地方官”并不是指在身体或精神上与他人有所不同，而仅仅是其公民处于一种特定的关系之中。

三种内涵定义

同义定义：提供另一个意义已被理解的词，而且它与被定义的词有相同的意义。人们学习外语通常使用同义定义。
操作定义：把被定义项通过一组可描述的动作联系在一起来解释另一个语词的内涵。仅仅涉及公共可重复的操作。
属加种差定义：如下
- 属：被分为子类的类是属。
  - 和类相同，所有给定属的所有元素都具有某些共同特征。
  - 每个子类的所有元素都具有更进一步的共同属性，而这些共同属性却不为任何其他子类的元素所共享
- 种：各种各样的子类都是种。
  - 一般的，一个给定属的所有种的元素共享某些属性，这些共享属性使它们成为该属的元素。
  - 任何一个种的元素都共享某些更进一步的属性，这些属性将它们与该属的任何其他种的元素区分开来，用来区分它们的性质叫种差。
- 属和种的关系是相对的，同一个类在关系上可以是它子类的属，也可以是它所从属更大类的一个种。这里的属和种作为相对属于的用法是逻辑学上的，和生物学的用法是不同的，不应该混淆二者。
- 利用属加种差定义：“六边形”的定义：它的属是多边形，种差具有六条边，利用属加种差定义而得到解释：“六边形”这个词的意思是“具有六条边的多边形”。
  - 通过属加种差定义一个词项需要经过两步：
    - 首先必须找出一个属：即包括被定义的那个种的较大的类。
    - 第二步找出种差：即将被定义的那个种的元素与那哥属的其他所有种的元素区分开来的性质。
  - 局限性：
    - 仅能用于那些暗含有复杂属性的词汇。如果是简单的不可再分析的属性，那么暗含这些属性的词汇就不能由属加种差来定义。（例如人们对颜色的认识）
    - 表达与“大全（universal）”性质的词汇有关，如“存在”，“本体”和“客体”等，这些词汇都不能通过属加种差的方法来定义。例如，所有本体的类就不是某个更大的属的一个种。大全类（universal class）是最高的类，或最高的属。
- 定义的五条规则
  - 规则 1：定义应当解释种的本质属性。也可以说“定义应当表明被定义项的规约内涵”
  - 规则 2: 定义不能循环。被定义项本身不能出现在定义项之中。已不能使用同义词或反义词。
  - 规则 3：定义不能过宽又不能过窄。构建适当的定义项，使之指谓的事物不比被定义项指谓的事物多或少。
  - 规则 4：定义不能用歧义的，晦涩的或比喻的语言来表述。比喻性的语言可以表达对被定义项的一种“情感”，却不能对被定义项给出一个清楚的解释。
  - 规则 5：定义在可以用肯定定义的地方就不应当用否定定义。定义是要说明一个词项确实具有什么意义，而不是说明它们没有什么意义。

总之，内涵性定义，尤其是属加种差的定义可以满足定义想要达到的各种目的，它们能帮助消除歧义，减少模糊性，给出理论的解释，甚至影响态度。

谬误

广义：在宽泛的意义上，任何推理上的错误都是谬误。

狭义：逻辑学家所使用的谬误指的不是推理中出现的任何错误，而只是那些典型错误 —— 出现在推理种，有某种模式，能够被识别和命名的错误。

每个谬误都是不正确论证的一种类型。犯有特定类型谬误的一个论证，也可以被称为一个谬误，也即那种类型错误的一个个例。

形式谬误：是以某种特定形式在演绎论证种出现的错误。

然而大多数谬误都是非形式谬误。非形式谬误产生于语言的含混性，我们很可能会被表面看似可信，实际上毫无根据的推理所蒙骗。

我们必须注意自己不要范这些错误，还需注意不要误判别人犯了推理错误。我们的逻辑标准应当高一点，将这些标准运用于日常生活的论证，也应当宽宏和公平。

非形式谬误

相干谬误：是最常见也是最多的一种谬误，该谬误中，论证所依据的前提与其结论不相干，然而它们被构造为看似相干。
- 诉诸情感
- 红色鲱鱼
- 稻草人
- 人身攻击
- 诉诸暴力
- 不得要领（不相干结论）
不当归纳谬误： 前提虽然与结论相干却太弱而缺乏力度，基于这些前提做出推论是愚蠢的。
- 诉诸无知的论证
- 诉诸不当的权威
- 虚假原因
- 轻率概括
预设谬误：在这类谬误中，前提中假定了太多东西，而推论又错误的依赖于前提的这些没有根据的假定。
- 偶然
- 复杂问句
- 丐题
含混谬误：该谬误起源于语词或表达式莫能两可的用法。有些语词或表达式在同一个论证的不同地方又完全不同的意思。
- 歧义
- 双关
- 重音
- 合成
- 分解

相干谬误

相干谬误是一种赤裸裸的错误。发生于一个论证所依据的前提于其结论没有真实关联，关联的确实，前提就不可能为其结论的真实性提供保证，这种论证的前提常常在心理上与结论是相干的，而错误就产生于以语言的情感特征支持结论而并未给出客观理由。

R1. 诉诸情感 (Argument Ad Populum)

原因是它用表达性语言和其他有计划的手段以博取情感，激起支持或反对某事的热情，而不是致力于提出证据和合理的论证。爱国主义是一种比较常见，容易激发起来的情感，我们也知道那些爱国主义名义之下的可怕虐杀与不公正行为。

加入情感的论证缺虽缺乏理智的元素，但是其结论可以得到超越理性的前提的支持。但是纯粹用情感作为前提，就是一种谬误。

作为一个论证之前提的情绪和作为激发某种行为的情绪之间是有区别的。但这种区分是有问题的，辩论中诉诸情感总是不可避免的。

我们不断的被这个时代的广告以各种诉诸情感的谬误所操纵。在这些糟糕的论证中，有一种论证尤其愚蠢——随大流，即诉诸于大众热情。

还有一种经常出现情感谬误叫诉诸同情（argument ad misericordiam），但一个论证的前提只是为了诉诸同情心，该论证显然是诉诸同情谬误。它的特殊性就在于所诉诸的是别人的慷慨和仁慈之心。

R2. 红色鲱鱼 (The Red Herring)

红色鲱鱼是一种其效力基于注意转移的谬误论证。在讨论中，听众被诱使专注于所讨论话题的某方面，即那些可能与讨论主题相关实际却与争论命题的真假无关的观点和现象，从而偏离了真正核心。

许多情景中，任何蓄意误导性线索一般都被称为红色鲱鱼。

R3. 稻草人 (The Straw Man)

将对方的立场解读为非常容易驳倒的论点再加以反驳，显然是一种谬误。这种论证就犯了稻草人谬误。

与红色鲱鱼的区别：是将不同阵营原本复杂的冲突转向新的不同冲突，而不是还停留在原来的争论中。

一般来说，稻草人论证都采取以下形式，假设要攻击的立场采用了最极端的观点，即任何行为或政策都会拒斥的观点。该论证很容易赢，但它的前提与预先假定的结论不相干。

稻草人攻击可能会招致听众在理智上转向被误读的那一边，因为听众可能会发现这种夸张描述中的不合理，对这种不公产生厌恶。

R4. 人身攻击 (Argument Ad Hominem)

在不相干谬误中，人身攻击论证是最为致命的谬误之一。论证的矛头并不针对结论，而是直指为结论辩护的人。

人身攻击的两个主要类别：

A. 诽谤：贬低对手的品格，否认他们的智力，质疑他们的正直等等。然而个人品格与他主张的命题在逻辑上并无关联。然而在心理上，诽谤可能是具有说服力的。促使听者将情感上的反对态度扩展之他的观点。
B. 背景谬误：将其背景当做相反论证的前提。如果仅仅因为对手的职业、国籍、政治关系或其他背景，就固执的迫使对手接受或拒绝某个几轮，这样的论证就是谬误的。

该人身攻击与断言的真假不相干，该人身攻击就是一个真正的谬误

R5. 诉诸暴力 (Argument Ad Baculum)

用威胁或强迫的方法来胁迫对手很难算是一种论证。无论暴力被真没为多便利，它仍然无法取代论证这一理性方法。

暴力威胁不必是武力，比如也能用利益来进行威胁。各种形式的暴力威胁从理性上都是不可接受的，诉诸暴力是对理性的抛弃。

R6. 不得要领 (Ignoratio Elenchi)

即前提和结论出现了“断裂”，一般情况下，该谬误是思维凌乱的产物，是由于其提出者没有完全理解争论中的命题而出现的混乱。也有可能是将这种歪曲作为精巧骗术的工具。

前提 “推不出（non sequitur）” 结论。

R7. 错误类比（false analogy）

错误类比（false analogy）、牵强比附、牵强类比、不当类比、或弱类比（weak analogy）是一种非形式谬误，系使用不恰当的类比推论而得出不恰当的结论。犯了这种谬误的人藉由比较两件不同事物在某些方面的共同点，来推论这两件不同事物在另外一些方面也必然相同。其具体的推论形式为：因为X和Y在a、b、c方面相同，所以X和Y在p、q、r方面也必定相同。

例一（不相干）
小朱整天只顾读书，却不认真赚钱谋生，妻子无法忍受决定和他离婚。几年后小朱成为大官，衣锦还乡。妻子要求和他复合，小朱把水泼在地上说：「我们的关系就像这水一样，再也收不回来了。」
如果小朱的意思是「覆水无法收回，因此我和妻子无法复合」，即是不当类比：覆水无法收回是自然定律，然而小朱是否愿意和妻子复合则是个人意愿问题。
例二（不充分）
艺术创作和色情书刊都有性和裸体。艺术创作没有十八禁，所以色情书刊也不该有十八禁。
性和裸体并非考量是否十八禁的唯一理由，艺术创作和色情书刊尚有其他重要差异，比如色情书刊以刺激性欲为主，艺术创作则不然。

不当归纳谬误

不但归纳谬误中前提和结论是相干的，只是这种相干及其不充分。

D1. 诉诸无知的论证 (Argument Ad Ignorantiam)

如果一个命题不能证明为假，就断定其为真，这便是诉诸无知论证，反之亦然。在科学中，如果无法找到某似真断言为真的证据就断定它为假，这便是诉诸无知谬误，反之亦然。

有人反对转基因食物的理由是：由于人类对基因的认识不足，所以转基因食物是危险的。在与此相似的环境中，我们依赖的不是无知而是我们的知识和信念，假如出现我们关心的结果，那么它在某些实验中就可能已经出现。这种以未能否证去确定真的作用，设定了研究者广泛的实验。

02. 诉诸不当的权威 (Argument Ad Verecundiam)

但诉诸的对象不能对所讨论的命题合理的宣传权威时，就会产生诉诸权威谬误。明星代言产品是一个典型的例子。

无论如何对某命题为真的断定以某人的权威为依据，而他在那个领域并没有特殊的能力，那么这种措置的诉诸权威就犯有谬误。

当然，即使一个人的确具有合法声称的权威，也可能会被证明出错。如果我们的结论是在以此权威意见为基础时，我们的错误就是一种推理错误即谬误。

03. 虚假原因 (Argument Non Causa Pro Causa)

即将实际上不是某事件的原因当作原因。设定一个并不真实存在的因果关系，我们简单称之为虚假原因谬误。

例如：日食时每次敲锣打鼓太阳的确会重新出现，但认为敲锣打鼓是日食之后太阳重新出现的原因是荒谬的，纯粹的时间连续不能建立一种因果联系。这种虚假原因被称为 “post hoc ergo propter hoc”

滑坡谬误：如果在一个虚假原因上前进，就一定会产生沿着该方向过度前进而产生的可怕后果。

04. 轻率概括 (Hasty Generalization)

我们终其一生都依赖于对人和事物的概括陈述，虽然概括陈述在推理中很有用，但是它们必须经过严格的审查，即没有辩护就不能接受或假设它们是普遍使用的。

从单个或很少例子道对所有例子或大多数例子的概括是错误的推理，但这种推理很常见也极具诱惑性。该错误也称逆偶然谬误。

预设谬误

掩藏在论证里的可以假设对支持结论非常关键时，论证就是糟糕的并可使人陷入误区。这类无根据的跳跃被称为预设谬误。
预设谬误来自于不可支持的暗含假定。

P1. 偶然 (Accident)

具体情况具体分析，总体上为真的概括却可能无法适用于某个给定的案例或特殊的环境中，该特殊环境又被称为那些例子的偶然环境，如果忽略这些偶然环境而认为概括能被普遍的使用，则犯了偶然谬误。

轻率的将个例进行概括，称之为逆偶然谬误. 而轻率的将一个概括用于个例之上,就犯了偶然谬误.

若把推理建立在某些规则普遍适用的假定上,就很可能是在进行谬误的论证.

P2. 复杂问句 (Complex Question)

最为常见的一种预设谬误是，它掩藏在问句中预设某些论断为真，以这种方式来问问题，并不是真正寻求问题本身的答案，这种问句的本身往往是修辞性的。偷偷的向问题引进其预设，常常可以利用预设谬误达到提问者的目的。

复杂问句常常是一种欺骗设置，提问者会提出一些问题，回答者可以先澄清问题再予以回答，即用解释问题中掩藏着的前提来回答。

在争论中，任何一个问句必须要回答“是和否”时，都有理由怀疑该问句是不是不正当的复杂问句。头条新闻中出现的问题就常常具有这样的目的。

当一个问句掩藏着多个预设时，就必须对它们逐个进行否定，仅仅否定一个可能会导致对其他假定的肯定。

P3. 丐题（Petitio Principii）

指的是要求或假定争论中的问题是得到承认的。这样的论证是没有价值的，这样的论证犯了明显的谬误。

例如：

没有不能诉诸实践的知识，因为不能诉诸实践的根本就不算知识。
学逻辑的人都是冷血动，因为学逻辑的人只会论理不讲情义。
因为每一个人都有充分而无任何限制的言论自由，对整个国家来说，已经受益无穷；因为每个人都享受到无拘无束，可以随意表达感触和思想，一定对社会有利无害。

一种论证，如果结论和前提的命题完全相同，用一模一样的字和词，自然不能欺骗任何人，但假如在形式上做点改变，（实际完全一样）就很容易使人上当。

丐题算不上是任何一种论证，因此不是谬误，因此称之为丐题。丐题从技术上通常是有效的，但也通常是无意义的。

含混谬误

一个词项在前提是一种意义，但是在结论又是另一种不同的意义，但推论依赖这样的变化时，这就是含混谬误，或“诡论（spohisms）”

A1. 歧义

大多数词汇有多于一个的字面意义，但人们有意无意地混淆一个词的几个意义时，就是在歧义的使用这个词。如果在论证中这样做就犯了歧义谬误

错误使用相对词（relative）项的谬误，例如高低，大小，好坏这些词，都是相对有效的。例如“象是动物，小象是小动物”；“有人论证某某是一位好将军，因此也会成为一位好总统。”；“因为你是个坏女人，所以你是个坏记者。”

A2. 双关

由于前提的语法结构原因，会导致其表达产生歧义。但人们从这样的前提处罚论证时，就会出现双关（amphiboly）谬误.

一个双关陈述在一种解释下可能是真的，而在另一种解释下却是假的。

A3. 重音

意义可能会由于对单个语词的不同强调而变动，若前提的意义依赖于一个可能的强调，但是，得出的结论却依赖于对相同词汇的不同强调，这就是重音（accent）谬误

重音谬误可以宽泛的解释为包括这样的曲解，即把引用的语段从其语境中拿出，再把它放入另一语境中，从而得出一个根本不能从其最初语境得出的结论。这种超出语境的引用有时是故意欺骗的。

例子：“我们不应当说朋友的坏话”

不同重音所导致的结论

“我们不应当说朋友的坏话” ：说那些不是我们朋友的人的坏话就不会被制止。
“我们不应当说朋友的坏话” ：虽不应当说坏话，但我们可以对朋友做坏事。

通常来说，一个短语只有在其语境明确的时候才能被正确理解。

广告中的 “全场【1折】起”，1折就写的非常大，后面跟个“起”字。还有新闻报道中被裁减的图片。

A4. 合成

第一类合成谬误：以作为整体之部分的性质得到整体本身性质的推理。

第二类合成谬误：对一个词项的分布式断言是真的，因而该词项的汇集式断言也是真的。

正如砖头的纯粹汇集不是房子，组织的整体与纯粹的汇集式截然不同的，所以这两种形式的合成谬误也是如此。一种是从部分到整体的无效推广，另一种是从元素到总体的无效推广。

A5. 分解

分解谬误是合成谬误的简单颠倒；

第一种分解谬误：断言对一个整体为真的东西一定对它的部分也为真。

第二种分解谬误：从元素汇集性质而得出元素自身的性质

古典逻辑

直言命题

演绎理论

旨在阐明有效论证的前提和结论之间的关系，为评估演绎论证提供方法。

类与直言命题

古典逻辑处理的主要是关于不同对象的类之间的关系的论证。两个类相互关联的三种方式：

一个类的元素都是另一个类的元素，则称第一个类包含于（wholly included）第二个类中。
一个类部分元素是另一个类的元素，则称第一个类部分地包含于（partially included）第二个类中。
两个类没有共同元素，则称这两个类之间是互斥（exclude）的.

演绎论证中，给出的命题都是陈述某个类与另一个类之间关系的，这样的命题被称为直言命题。即它们都肯定或否定了某个类S全部或部分的包含于另一个类P之中。

四种直言命题

有且只有四种标准直言命题：

全称肯定命题(A 命题)： 所有S是P. 断言第一个类的元素都是第二个类的元素. S-主项 P-谓项
全称否定命题(E 命题)：没有S是P
特称肯定命题(I 命题): 有S是P. 解释为“至少有一个S的元素也是P的元素”
特称否定命题(O 命题): 有S不是P 至少有一个S元素不是P元素

质、量与周延性

质：一个命题不管是部分肯定还是全部肯定（A 和 I 命题），它的质就是肯定的。要么就是否定的 (E 和 O 命题)

量：如果一个命题述及主项所指称类的所有元素，那么它的量就是全称的 (A 和 E命题)，如果只涉及某些元素，它的量就是特称的

联项：主项联项谓项，联项除了是和不是之外，依据措辞需要，也可能是其他形式。

周延性：用以刻画出现于直言命题中的主谓项的性质，如果一个命题述及了某个词项所指称的类的全部元素，则该词项在这个命题中是周延的。

量决定主项的周延，全称命题，主项周延，特称命题，主项不周延。

质决定了谓项的周延。肯定命题谓项不周延，否定命题，谓项周延。

命题	名称	量	质	周延性
所有S是P	A	全称	肯定	仅S周延
没有S是P	E	全称	否定	S、P都周延
有S是P	I	特称	肯定	S、P都不周延
有S不是P	O	特称	否定	仅P周延

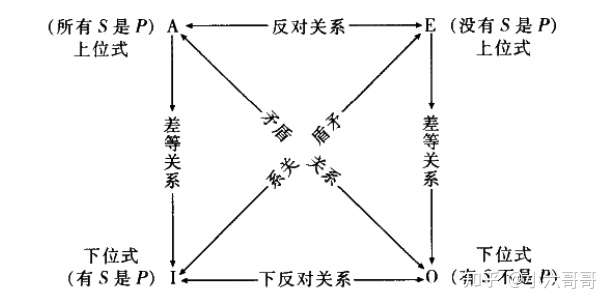
传统对当方阵

对当关系（opposition）：具有相同主项和相同谓项的标准式直言命题，可能在量上不同，或者在质上不同，也可能在质与量上都不同，以上三种不同中任何一种都传统的被成为对当关系。

A. 矛盾关系（Contradictories）: 两个命题一个是另一个的否定（negation）或拒斥（denial），它们既不能同真也不能同假。如果两个命题是对当关系，而质量都不同，那么它们就是矛盾的，例如A和O，E和I。即不可同真，也不可同假的关系。由其中一个命题的真，必然推出：另一个命题的假。由其中一个命题的假，也必然推出另一个命题的真。

B. 反对关系(Contraries): 可以同假，但不可同真的关系。由其中一个命题的真，可以必然推出另一个命题的假，但由其中一个命题的假，却不能必然推出另一个命题的真。

C. 下反对关系(Subcontraries): 两个命题必有一真，可以同真。由其中一个命题的假，可以必然推出另一个命题的真。

D. 差等关系(Subalternation): 如果全称命题为真，那么特称命题一定为真；如果特称命题为假，那么全称命题一定为假。

E. 对当方阵图

其他直接推论

A. 换位法

仅仅通过交换命题中主谓项的位置进行推论。

有效换位表

被换位命题	换位命题
A: 所有S是P	I:有P是S （限制换位）
E: 没有S是P	E: 没有P是S
I: 有S是P	I: 有P是S
O: 有S不是P	（换位无效）

限制换位：通过差等关系和换位法的结合，从所有S是P就可以有效推出有P是S。

B. 类和补类

补类(complement)：即不属于原来的类所有东西的汇集。人类的补类就是非人类。

C. 换质法（Obversion）

对一个命题改变其质，并用谓项的补类替换原来的谓项，主项保持不变，量也不需要改变。

换质表

被换质命题	换质命题
A: 所有S是P	E: 没有S是非P
E: 没有S是P	A: 所有S是非P
I: 有S是P	O: 有S不是非P
O: 有S不是P	I: 有S是非P

D. 换质位法

对一个命题进行换质位，并将谓项换为原命题的补。

换质位表

前提	完全换质位命题
A：所有S是P	A：所有非P是非S
E：没有S是P	O：有非P不是非S（限制）
I：有S是P	（换质位无效）
O：有S不是P	有非P不是非S

存在的含义与直言命题的解释

存在含义：如果说出一个命题就肯定了某种对象的存在，那么就说这个命题有存在含义。

A命题：所有火星人都是金发碧眼

O命题：有火星人不是金发碧眼

如果没有火星人，则两个命题都是假的，他们就不可能是矛盾关系。

对于一个不能明确断定其中有元素的类，我们就不能假定它有元素，否则就是错的。任何一句这种错误假定的论证都会产生存在预设谬误，简称存在谬误

布尔的解释中 “所有火星人都是金发碧眼的”断定的是“如果有火星人，那么，他们是金发碧眼的”。这种 “如果…那么…” 型的命题，都可以为真。

布尔解释下差等关系无效。其基础是一个全称命题推出一个特称命题，全称命题并不肯定类中有元素，但特称命题却做了这种肯定，这就犯了存在谬误。

直言命题的符号系统与图解

0 表示空类，S =0 表名该词项的S指称的类没有元素。（S的元素记为 S’s） S ≠ 0 表示存在S’s, 就是对S为空的否定。

S 代表所有“讽刺作品”的类，P代表所有“诗”组成的类，那么即是讽刺作品，有是诗的类，用SP表示，代表所有的讽刺诗。两个类的共同部分或全体共同元素成为两个类的积(product)或交(intersection) SP=0

E命题：没有S是P 可以表示成 SP=0

I命题：有S是P 可以表示为 SP≠0 或

O命题：有S不是P 可以表示为 SP≠0 上划线表示非P类

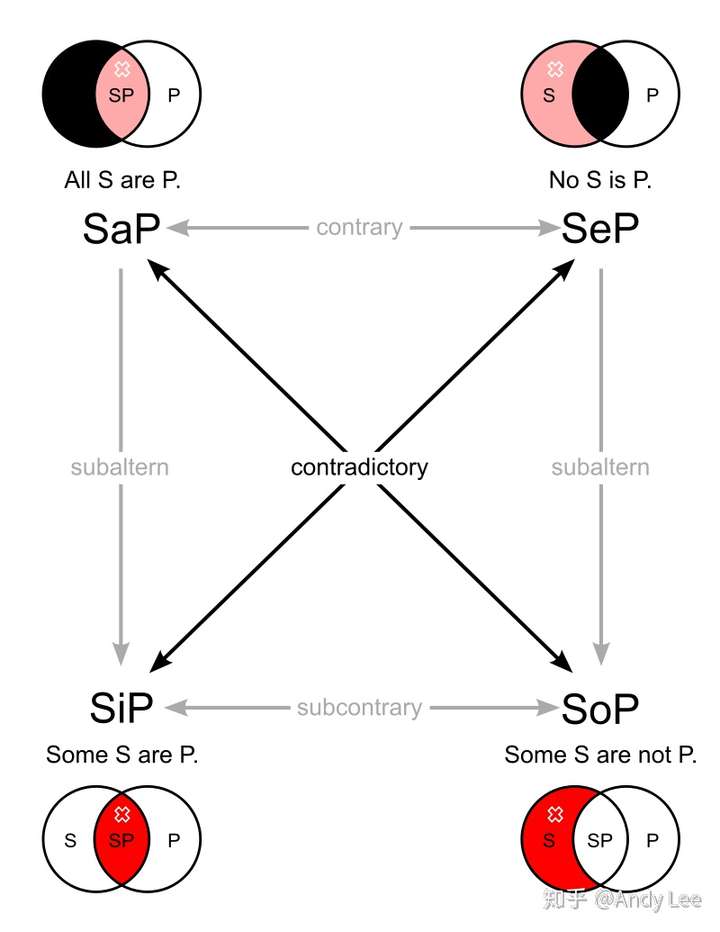
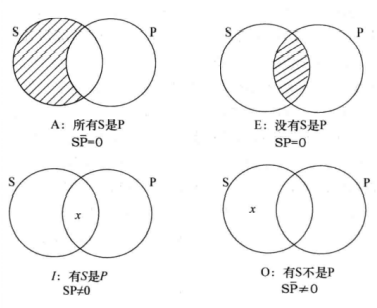
直言命题符号表达

形式	命题	符号表达	解释
A	所有S是P	SP=0	S和非P的积为空
E	没有S是P	SP=0	S和P的积为空
I	有S是P	SP≠0	S和P的积非空
O	有S不是P	SP≠0	S和非P的积非空

对当方阵

ven

标准直言三段论

基于 A、E、I、O 命题的论证通常包含两个直言命题作为前提，一个直言命题作为结论。这种论证被称为三段论

直言三段论：基于类或概念之间关系的论证，由三个直言命题组成的演绎论证，其中仅包含三个词项，每个词项在其构成命题中恰好出现两次。

标准直言三段论的组成

大项结论的谓项

小项结论的主项

中项在两个前提中都出现，却不出现在结论中的项

大前提包含大项的前提

小前提包含小项的前提

大前提处在第一项，小前提处在第二项，结论在最后。

三段论的式：以命题类型而定。例如：EIO式

三段论的格：

所有P是M
有S是M
——————————
∴ 有S是P

三段论根据中项在前提中的位置分为四种不同的格

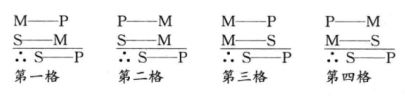
上面的三段论可以表示为 AII-2

三段论的形式性质

三段论的有效性和无效性取决于形式。

例如任何形式为AAA-1三段论

所有M是P
所有S是M
________
∴ 所有S是P

无论其题材是什么，都是有效论证。

Venn 图解法

当出现有x时，x 应标注在第三格对象的分界线上面

直言三段论练习题

1.有改革者是狂徒，所以有理想主义者是狂徒，因为所有改革者是理想主义者。

2.有哲学家是数学家，因此有科学家是哲学家，因为所有科学家是数学家。

3.有哺乳动物不是马，因为没有马是人头马，且所有人头马是哺乳动物。

4.有神经病人不是被监护人，但所有罪犯是被监护人，所以可知有神经病人不是罪犯。·

5.所有水下船只是潜水艇，因此，没有潜水艇是游艇。因为没有游艇是水下船只。

6.从来没有罪犯是拓荒者，因为所有罪犯是恶人，而从来没有拓荒者是恶人。

7.没有音乐家是宇航员，所有音乐家是篮球迷，因此，没有宇航员是篮球迷。

8.有基督徒不是卫理公会派教徒，因为有基督徒不是新教徒，而有新教徒不是卫理公会派教徒。

9.没有想赢得大选的人是真正的自由党人，所有活跃的政客是想赢得大选的人，因此，没有真正的自由党人是活跃的政客。

10.没有怯懦者是工人领导，因为没有怯懦者是真正的自由党人，并且所有工人领导是真正的自由党人。

三段论规则和谬误

三段论谬误属于形式谬误

规则一：避免四项。即主项与谓项还有中项。必须只有三个项，不能多也不能少。

规则二：中项至少在一个前提中周延。这样的谬误称为中项不周延谬误

规则三：在结论中周延的项在前提中也必须周延.如果前提不周延的项在结论中周延，也就是结论断定了比前提更多的东西，这样的谬误称为不当周延。

规则四：避免出现两个否定前提。

规则五：如果一个前提是否定的，那么结论必须是否定的。

规则六：两个全称前提得不出特称结论

直言三段论的15个有效形式

三段论的式有 64 种。格有4格，两个结合起来，直言三段论公有256种格式。只有15种格式是有效的。

AAA-1 Barbara
EAE-1 Celarent
AII-1 Darii
EIO-1 Ferio
AEE-2 Camestres
EAE-2 Cesare
AOO-2 Baroko
EIO-2 Festino
AII-3 Datisi
IAI-3 Disamis
EIO-3 Ferison
OAO-3 Bokardo
AEE-4 Camenes
IAI-4 Dimaris
EIO-4 Fresison

日常语言中的论证

日常语言的三段论与标准直言三段论存在的三种偏离

日常论证的前提和结论顺序不标准。可以通过调整前提得到补救，大前提放第一位，其次是小前提，最后是结论。
标准三段论有且仅有三个谓词。日常语言论证如果不失掉原意，项的数量能够减少为三个，那么该论证就有可能成功归化为标准三段论
日常语言论证构成的命题不都是标准直言命题。这种偏离很常见，如果在没有意义丢失的前提下，这些命题能转化为标准形式，那么该论证就有可能成功归化为标准三段论

理清楚这些偏离之后，就可以对它们进行化归。

词项数量的规约为三的方法

去除同义词。没有富人是游民，所有律师都是有钱人 -> 没有富人是游民，所有律师都是富人
去除补类。没有非居民是公民 -> 所有公民都是居民

直言命题标准化的方法

一: 单称命题

有些肯定火否定的是一个特定的个体或对象属于某个类。例如“苏格拉底是哲学家”，“杨太君是三瓣嘴”，这样的命题叫做单称命题。它们肯定或否定的不是一个类与另一个类的包含关系（像标准直言命题那样），我们可以把单称命题解释为处理类与类间关系的命题。一般会把单称命题当做全称命题来处理，即归到A、E命题。但是全称命题没有存在含义。

如果把“s是P”当做“所有S是P”，那么就丢掉了单称命题的存在含义。如果当做“有S是P”，有漏掉了单称命题的全称性，即主项周延，它所说的是全部S是P。

解决此问题的办法就是把单称命题分析为两个直言命题的合取，即一个单称命题等价于两个相互关联着的A、I命题的合取。这样”s是P”等价于“所有S是P”合取“有S是P”。文恩图表示如下：

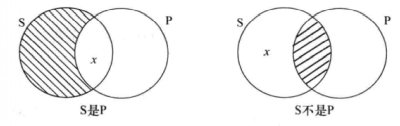
二：谓词为形容词或形容词短语，而非名词或类词项的直言命题

例如“花是美的”，“没有战船是可调用的”。但“美的”和“可调用的”表示属性而不是类。不过每个属性可以确定一个类，即具有这种属性的事物组成的类。“有花是美德事物”，“没有战船是可调用的事物”

三：主要动词不是标准的联项“是”或“不是”的直言命题。

例如“所有人都寻求赞誉”，“有人喝白酒”。转化的方法是把主项或量项之外的所有成分看成类定义特征所确定的类，再改用标准的联项把它们通主项联结起来。“所有人是赞誉的寻求者”，“有人是白酒饮用者”

四：标准形式的各成分都出现却没有按照标准顺序排列的陈述句

“赛马全是良种马”和“结果好的事总是好事” 可翻译为“所有的赛马是良种马”和“所有的结果好的事是好事”

五：量词不是“所有”、“没有”和“有”这些标准词的直言命题。

所有：每一个，全部，任何，任一
没有：不会有，不管是谁
有：有个

六：排斥命题

含有“只”，“只有”的直言命题通常叫做排斥命题。例如“只有公民能成为选民” -> “所有能成为选民的是公民”。

因此“只有S是P” 和 “只有S’s是P’s” 通常被理解为 “所有P是S”, 在某些语境中，“只”，“只有”表达更多的含义，这种情况并不常见，这个时候就要依照语境而定了。

七：不含量词的直言命题

例如“狗是肉食动物”、“孩子在场” 只有考察它们所处的语境才能确定其含义。一般，第一个例句是“所有的狗都是肉食动物”，第二个一般只述及某些孩子“有孩子是在场的人”

八：完全不像标准式直言命题但也可以有标准时翻版的命题

“不是所有的孩子都相信圣诞老人” -> “有孩子不是相信圣诞老人的人”
“有白色的大象” -> “有大象是白色的事物”
“没有粉色的大象” -> “没有大象是粉色的事物”

九：除外命题

“除了雇员都是合格的”
“雇员之外的人都是合格的”

所有非雇员是合格者，并且没有雇员是合格者

“几乎所有”，“并非全部”，“除少数几个之外都”，“几乎每个人”等含有数字量词的推理也可以用三段论分析。

除外命题不是直言命题，而是合取式。

如果一个论证中有一个前提是除外命题，那么对其有效性的检验要分量词，即分别对两个不同标准式的直言三段论进行检验。如果前提是直言命题，但结论是除外命题，那么我们就可以断言它是无效的。

每个看过比赛的人都参加了舞会，
不是全体学生都参加了舞会，
__________________________
所以，有学生没有看过比赛。


所有看过比赛的人都是参加了舞会的人，
有学生是参加了舞会的人，
__________________________
所以，有学生不是看过比赛的人。

AIO-2 False 中项不周延

所有看过比赛的人都是参加了舞会的人，
有学生不是参加了舞会的人，
———————————————————————————
所以，有学生不是看过比赛的人。

AOO-2 True Baroko

协同翻译

引入参项：你总是与穷人为伍。“总是”意味着“在所有时间”，表名原命题的一种标准式翻译为：“所有时间都是你与穷人为伍的时间”

对三段论的三个命题构成进行协同翻译的过程中，参项引入是必不可少的。

省略式三段论

三段论很常用，但其前提和结论并不总是都得到明确的陈述。

比如“琼斯是个土生土长的美国人，所以琼斯是美国公民”。加上被省略的前提，完整的论证是

所有土生土长的美国人是美国公民
琼斯是土生土长的美国人
——————————————————————————————
所以，琼斯是美国公民

AAA-1 Barbara 有效论证。

如果一个推理是不完整的，其中有一部分需要“领会”，我们就称为省略式三段论

日常许多推论都是省略式的，因为有相当一部分命题是公共知识，亚里士多德《修辞学》中写道：“基于省略三段论的……演讲更受人欢迎”，但如果要检验其有效性，必须找到被省略的部分，缺少省略的前提，该论证就是无效的。

三段论的三种省略体：

不出现大前提。如上面的例子
保留大前提和结论，而不出现小前提。“所有学生都反对新规则，所以，大二学生都是反对新规则的”
前两个前提都出现，但未表述结论。“没有真正的基督徒是精神空虚的，但有些常去教堂礼拜的人是精神空虚的” 省略的结论是“常去教堂礼拜的人不是真正的基督徒”，第三种省略体，在某些情况下不结合语境也能看出是无效的。例如-两个前提都是否定的，或都是特称的，或者中项不周延。

有些三段论无论补上什么样的前提，即使是不合理的前提，也不能成为有效三段论。省略三段论与普通三段论本质上是修辞上的，而不是逻辑上的，它们终究要接受与标准直言三段论同样的检验。

连锁三段论

有时，仅靠一个三段论，不足以说明我们如何从一组前提中的出结论。如果推理用省略式表述，只给出前提和最后结论，这就是连锁三段论，可以有任意多个前提。一个论证链的有效性取决于各论证环节都是有效的。

例如：所有外交家都是精明人，有些政府官员是外交家，所有的政府官员是公众人物，所以有些公众人物是精明人。

所有外交家是精明人
有政府官员是外交家
————————————————————
所以，有政府官员是精明人 (AII-1 Darii)
所有政府官员是公众人物
————————————————————
所以，有公众人物是精明人 (IAI-3 Disamis)

析取三段论

直言命题都是肯定或否定概念之间的包含或排斥关系的命题。

直言命题在只包含单子组成部分的意义上是简单命题，有些三段论使用的命题是包含多个支命题的复合命题。

第一种复合命题：析取命题（disjunctive）或选言命题。

例：“她或者是受愚昧所驱使或者受傲慢所驱使”，包含两个支命题，析取命题并非直接肯定某个支命题为真，而是说它们当中至少有一个是真的，也不排除两个同时为真。

只有用一个直言前提否定析取前提的一个析取支，从而肯定另一个析取支时，我们才说它是一个有效的析取

在试图掩盖她自己的不法行为或与之摆脱关系的过程中，她或者是受愚昧的驱使或者被傲慢所驱使。
显然她不愚昧，
——————————————————————————————————
所以她的窘境皆源自于她的傲慢。

假言三段论

第二种符合命题：条件命题（conditional）或假言（hypothetical）命题

“如果第一个土著人是政客，那么第一个土著人说谎”。 “如果”后面的命题叫前件(antecedent),“那么”后面的命题叫后件(consequent).

纯假言三段论

如果三段论所含的命题都是条件命题，成为纯假言三段论

如果第一个人是政客，那么他说谎。
如果他说谎，那么他否认自己是政客。
————————————————————————————————
所以，如果第一个土著人是政客，那么他否认自己是政客。

混合假言三段论

由一个条件前提和一个直言三段论组成的三段论叫做混合假言三段论

肯定前件式（affirmative mood）或分离式(modus ponens)

直言前提是对条件式前提的肯定，结论是对后件的肯定。

如果第二个土著人说真话，那么只有一个土著人是政客。
第二个土著人说真话。
——————————————————————————————————————————————
所以，只有一个土著人是政客。

肯定后件谬误 (fallacy of affirming consequent)：指其直言前提肯定的是条件前提的后件的论证

否定后件式(modus tollens)

其直言前提是对条件前提后件的否定，结论是对前件的否定，任何有这种形式的论证是有效的。

如果独眼犯人看见的是两顶红帽子，那么他就能说出自己所戴帽子的颜色。
独眼犯人不能说出自己所戴帽子的颜色。
————————————————————————————————————————————
所以，独眼犯人看见的并不是两顶红帽子。

否定前件谬误：指其直言前提否定的是条件前提的前件的论证

两难推论

不严格的说，如果一个人必须在两种选项中做出决断，但两个选项都是糟糕的，那么，我们就说这个人陷入了“两难”之中。

它实质是一种组合关于同一话题的三段论的争辩方法，有时甚至会产生压倒性效果。如此结合的三段论的前提都被构造为互相析取的，进而以某种方式迫使对手接收其中的析取支，因此对手就被迫接受结合在一起的三段论中的某个结论。

此宣言如同法律一样，或者有效或者无效。如果无效，就没必要取消。如果有效，就不能取消。任何人都明白。

避开或驳斥两难推论的结论方法：

一：绕过死角法

这是最常用的最容易避开二难的手段。除非析取前提的两个支命题是矛盾关系，否则它们很有可能是假的。

如果学生喜爱学习，那么就不需要激励。如果学生厌烦学习，那么激励也没有用。学生或者是喜爱学习或者是厌烦学习，所以，激励是不需要的或者没用的。

该论证形式有效，其析取前提可能是假的，因为学生会有不同的学习态度，有的喜爱，有的厌烦。还有许多人不同于两者，对于后面这些人来说，激励既是需要的，也是可以发挥作用的。这种方法并不是证明结论为假，只是表名推论本身并没有给结论提供充足的理由。如果析取前提穷尽了所有可能性，绕过死角法是不可驳倒的，必须用另外的方法。

二：直角一击法

我们只需要否定其中的一个即可，就是要试图表明条件前提至少一假。

“如果学生喜爱学习，那么就不需要激励”，反驳者可以争辩说即使一个学生喜爱学习，也需要激励，好分数带来额外的激励。

三：构造反二难法

这是最巧妙的方法，但并不总是能令人信服。用这种方法驳斥给定的二难推论，需要构造另一个二难推论，它的结论与原来的结论相反。辩驳中可以使用任何一个二难推论，但最理想的反二难推论应当与原来的推论有相同的组成成分。

例：相传雅典有一位母亲劝儿子不要从政时说道：

如果你主持公道，人们就会仇视你。如果你不主持公道，神灵们就会仇视你。你必定或者主持公道或者不主持公道，所以无论如何都会被仇视。

他儿子反驳倒：

如果我主持公道，神灵们就会施爱于我。如果我不主持公道，人们就会施爱于我。我必定或者主持公道或者不主持公道，所以我都会被爱。

反二难推论作为强力工具在日常辩论中，实际上并没有达成真正的反驳，仅仅是构建了一个结论不同的论证而已，但在唇枪舌剑的辩论中，并不需要细致的分析。

现代逻辑

符号逻辑

为了解释演绎论证中前提和结论之间的关系，和提供区分有效演绎和无效演绎的技术。有两大逻辑理论分支达到上述目标：一是古典逻辑 (或亚里士多德逻辑)，另一个是现代逻辑（或现代符号逻辑）

A 合取

陈述之间使用 and （“和”，“并且”），如此被连接的两个陈述叫合取支。合取符号用“ · ” 作为合取符号。p 和 q 代表任意两个陈述，他们的合取写为 p · q 。

注意：“林肯和格兰特是同时代人”不是一个合取，而是一个表达关系的简单陈述。

合取是真值函项的复合陈述，其合取支时它的真值函项的分支。如果它的两个合取支都是真的，该合取就是真的，否则它就是假的。

真值函项的复合陈述：陈述的所有分支被任何有相同真值但互相区别的陈述替换，其所得不同复合陈述相互之间有相同的真值。

如果一个合取的所有合取支都有相同的谓项，该合取通常被写成在两个主项之间加“和”而不重复谓项。

圆点 · 符号就是一个真值联结词, T 代表真 F 代表假

B 否定

连接词：并非

符号 ~

C 析取

连接词：或

符号 ∨

不相容析取：断言至少其中有一个为真，但并非两者都为真（除非意指不相容析取，吧）

D 标点符号

S · (P∨F)

() 和数学中的类似，先算括号内，再算括号外

条件陈述和实质蕴含

“如果……那么……” 如此构成的复合陈述是一个条件陈述，也叫假言陈述

蕴含：条件陈述句式有些蕴含逻辑，有些蕴含定义，有的蕴含因果关系，有的陈述某些特定情形下的决策

仅当一个条件陈述前件为真后件为假时，该条件陈述本身就被证明为假。因此可以推出条件陈述句式为真的条件是 ~(p · ~q)

符号 ⊃

如果p 那么q ，表示为 p⊃q

针对 p⊃q 而言，它不是前面任何一种蕴含，它被逻辑学家叫做实质蕴含。它是一个特殊概念，不应该把它和其他更常见的理性混淆。

如果世界是平的，则月亮是圆的。

虽然其逻辑上有问题，但实质蕴含为真，这就是实质蕴含的特殊性。

并非一定是“如果……那么……”句式，一般的说 q是p的必要条件和p仅当q 也可以符号化为 p⊃q。

如果p是q的一个充分条件，我们就有 p⊃q，并且 q 必定是 p的一个必要条件。如果p是q的一个必要条件，我们就有 q⊃p。因此，如果p是q的必要且充分条件，那么q是p的充分且必要条件。轿车行驶仅当它的油箱里有油。油箱里有油是轿车行驶的一个必要条件。

要注意并非每个含有“如果”类似词语的陈述都是条件陈述。

p	q	~q	p · q	p∨q	p⊃q
T	T	F	T	T	T
T	F	T	F	T	F
F	T	F	F	T	T
F	F	T	F	F	T

论证形式与逻辑类推进行的反驳

论证形式：用来检验论证的有效性。

用逻辑类推进行反驳如下命题：

1
2
3

如果培根写了那些通常归功于莎士比亚的剧本，那么培根是一位伟大的作家。
培根是一位伟大的作家。
因此，培根写了那些通常归功于莎士比亚的剧本。

你可以反驳说：你是否也可以这样来论证，

1
2
3

如果华盛顿是被暗杀的，那么华盛顿死了。
华盛顿死了。
因此，华盛顿是被暗杀的。

因为在这里，已知前提为真且结论为假，这个论证显然是无效的。

逻辑类推进行反驳的特点：

构造另外一个与原来论证有完全一样的形式的论证。
它有真的前提和假的结论

这种方法建立有效性和无效性是论证的纯粹形式的特征。

用符号表示上述的论证形式表示为：

1
2
3

p⊃q
q
∴p

无效论证和有效论证的含义

无效论证：一个论证形式是无效的，当且仅当，它至少有一个前提为真且结论为假的代入类。
有效论证：一个论证有效，当且仅当，该论证的特征形式是一个有效论证形式。
逻辑类推的原理：建立在一个无效论证形式上的任何论证，都是无效论证。任何一个不是无效的论证形式必定是有效的。

用真值表验证论证形式

根据以上真值表来验证论证形式。

常见的论证形式

常见的有效形式

析取三段论(D.S.)
1
2
3
pVq
~p
∴ q
肯定前件式(M.P.)
1
2
3
p⊃q
p
∴ q
否定后件式(M.T.)
1
2
3
p⊃q
~q
∴~p
假言三段论(H.S.)
1
2
3
p⊃q
q⊃r
∴p⊃r

常见的无效论证形式

肯定后件谬误
1
2
3
p⊃q
q
∴ p
否定前件谬误
1
2
3
p⊃q
~p
∴ ~q

一个有效的论证形式只能以有效论证作为代入例。也就是说，一个有效形式的代入例必定有效。

陈述形式与陈述

p V q 是陈述形式，因为若用陈述代入 p 和 q，就会产生一个陈述。

pVq 叫做析取陈述形式
p.q 叫做合取陈述形式
p>q 叫做条件陈述形式
~p 叫做否定形式

通用代入每个不同的陈述变元，就可以从其产生该给定的陈述形式。

重言式：只有真代入例的陈述形式 p|~p
矛盾式：只有假代入例的陈述形式 p&~p
偶真陈述形式：其代入例有真也有假。例如 p、~p、p.q、和p>q 都是偶真陈述请示。

实质等值

陈述形式不同但结果相同，则两个陈述就是实质等值的。

符号: ≡ ⇔ ↔ 读作当且仅当。

例如：我去看比赛，当且仅当，我获得入场券。当我获得了入场券，我会去，仅当我获得入场券我才能去。

若已知A和B两个陈述实质上等值，既可以推出条件陈述 A⊃B 的真，也可以退出条件陈述 B⊃A的真。由于实质等值成立时，蕴含是双向的。因此 A ⇔ B 的陈述通常称为双条件陈述。

论证、条件陈述与重言式

每个论证都对应这样一个条件陈述：它的前件是该论证的前提的合取，它的后件是该论证的结论。

1
2
3

p⊃q
p
∴q

可以被表达称一个具有形式[(p⊃q)&p]⊃q的条件陈述

逻辑等值

p⊃q = (~pVq)

演绎方法

推论规则

假言三段论(H.S.)
否定后件式(M.T.)
析取三段论(D.S.)

有效形式证明示例：

论证：

如果安德逊被提名，那么她会去波士顿。
如果她去波士顿，那么她会在那儿竞选。
如果她在那儿竞选，她会遇到道格拉斯。
安德逊没有遇到道格拉斯。
或者安德逊被提名，或者某个更合适的人被选中。
因此，某个更合适的人会被选中。

符号表达式：

A⊃B
B⊃C
C⊃D
~D
AVE
∴E

形式证明

1. A⊃B
2. B⊃C
3. C⊃D
4. ~D
5. AVE
   ∴E
6. A⊃C    1,2,H.S.
7. A⊃D    6,3,H.S.
8. ~A     7,4,M.T.
9. E      5,8,D.S.

有效性形式证明的定义

一个论证有效性的形式证明定义：它是一个陈述序列，其中的每个陈述要么是该论证的前提，要么是根据基本有效论证由该序列种前面的陈述推导出来的，使得该序列中的最后一个陈述为该论证的结论。我们的目标就是构造这样的一个序列，来证明所面对的论证的有效性。

有效性形式证明的构造

请论证

1
2
3

D⊃E
D·F
∴E

解：

1. D⊃E
2. D·F    /∴E
3. D      2, Simp.
4. E      1,3, M.P.

研究逻辑的目标是评价自然语言

有效论证形式

基本有效论证形式

析取三段论(D.S.)

1
2
3

pVq
~p
∴ q

肯定前件式(M.P.)

1
2
3

p⊃q
p
∴ q

否定后件式(M.T.)

1
2
3

p⊃q
~q
∴~p

假言三段论(H.S.)

1
2
3

p⊃q
q⊃r
∴p⊃r

构造式二难(C.D.)

1
2
3

(p⊃q)·(r⊃s)
pVr
∴ qVs

吸收律(Abs.)

1 2	p⊃q ∴p⊃(p·q)

简化律(Simp.)

1
2

p·q
∴p

合取律(Conj.)

1
2
3

p
q
∴p·q

附加律(Add.)

1
2

p
∴pVq

替换规则

德·摩根率 (De M.)

1 2	~(p·q) ≡ (~pV~q) ~(pVq) ≡ (~p·~q)

交换律 (Com.)

1 2	(pVq)≡(qVp) (p·q)≡(q·p)

结合律 (Assoc.)

1 2	[pV(qVr)]≡[(pVq)Vr] [p·(q·r)]≡[(p·q)·r]

分配律 (Dist.)

1 2	[p·(qVr)]≡[(p·q)V(p·r)] [pV(q·r)]≡[(pVq)·(pVr)]

双重否定律 (D.N.)

p ≡ ~~p

易位律(Trans.)

1	(p⊃q)≡(~q⊃~p)

实质蕴含律(Impl.)

1	(p⊃q)≡(~pVq)

实质等值律 (Equiv.)

1 2	p⇔q ≡ [(p⊃q)·(q⊃p)] p⇔q ≡ [(p·q)V(~p·~q)]

输出律 (Exp.)

1	[(p·q)⊃r] ≡ [p⊃(q⊃r)]

重言律 (Taut.)

1 2	p ≡ (pVp) p ≡ (p·p)

自然演绎系统

形式证明是一个关于有效性(effective)概念，意思是说，根据给定的推论规则表，可以在有限步骤内机械的判定一个给定陈述序列是否构成一个形式证明。这里不需要任何思维，即不需要思考序列中陈述的“意义”，也不需要用逻辑直觉来检查任何步骤的有效性。

无效性判断

如果一种真值指派使得一个论证的所有前提为真而结论为假，那么，这表明该论证是无效的。

量化理论

量化是德国逻辑学家弗里格首次引入。

由于还有许多有效演绎论证无法通过以上的逻辑技术来检验，之前的论证形式只能处理复合陈述，却无法处理非复合陈述。量化理论就是解决这个问题的。

单称命题

“苏格拉底是人” 这种类型的陈述传统上叫做单称命题，一个肯定的单称命题断言的是一个特定的个体具有某种特定属性。

“苏格拉底”是个体，人是属性。

个体用 a 到 w 的小写字母指谓，这些符号是个体常源。用大写字母符号化个体可能具有的属性。约定：把属性符号写在个体符号的左边，表示被命名的个体具有规定的属性。于是，单称命题“苏格拉底是人”可以符号化为 Hs

Hx 或 H(x) 成为命题函项，通过代入x 形成一个陈述。任何单称命题都是一个命题函项的代入例，是用个体常元代入该命题产生的结果。一个命题函项有真代入例和假代入例，并且每个代入例都是一个单称肯定命题

全称命题（普遍命题）

命题一： “所有的事物都是会死的” 这个命题的定义过程

1. 所有的事物都是会死的。
2. 每个事物都是会死的。（逻辑等价）
3. 给定任何一个事物，它都是会死的。（逻辑等价）
4. 给定任何x, x是会死的(用变量 x 代替代词它)
5. 给定任何x，Mx (用单称肯定命题的符号表示)
6. (x)Mx (给定任何x用符号"(x)"表示)

(x)Mx 表示所有的事物都是会死的。

命题二：有些事物是漂亮的

1. 有些事物是漂亮的
2. 至少存在这样一个事物，它是漂亮的。
3. 至少存在这样一个x，它是漂亮的
4. 至少存在这样一个x，Bx
5. (∃x)Bx (∃ 表示存在)

(∃x)Bx 表示有些事物是美丽的

命题三：没有事物是完美的

(x)~Px

命题四：有些事物不是会死的

(∃x)~Mx

全称量词和存在量词的相互关系 Φ 表示属性（谓词）

[(x)Φx]≡[~(∃x)~Φx]
[(∃x)Φx]≡[~(x)~Φx]
[(x)~Φx]≡[~(∃x)Φx]
[(∃x)~Φx]≡[~(x)Φx]

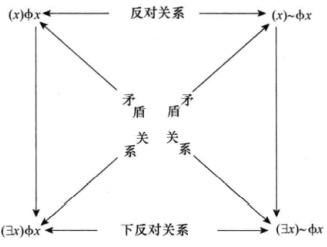
反对关系：同时为假，但不能同时为真
下反对关系：同时为真，但不能同时为假
矛盾关系：其中一个为真，另一个必然为假
方阵的两侧，下面命题的真被它正上方命题的真所蕴含。

主谓命题

【A命题】所有人都是会死的。

1. 所有人都是会死的
2. 给定任何事物，如果它是人，它是会死的
3. 给定任何x，如果x是人，那么x是会死的
4. (x)(Hx⊃Mx)

Φ Ψ 表示任何一个谓词

A: (x)[Φx⊃Ψx]
E: (x)[Φx⊃~Ψx]
I: (∃x)[Φx·Ψx]
O: (∃x)[Φx·~Ψx]

有效性证明

1
2
3

所有人都是会死的
苏格拉底是人
所以苏格拉底是会死的

符号化：

1
2
3

(x)(Hx⊃Mx)
Hs
∴Ms

根据肯定前件式，得出Ms

全称列举原则 U.I.

一个命题函项的任一代入例都可以有效的从其全称量化式推得，那么这种推论规则就是全称列举原则，简写“U.I.”

1 2	U.I.: (x)(Φx) ∴Φν

ν 表示任一个个体符号。

其有效性的形式证明可写成

1. (x)(Hx⊃Mx)
2. Hs
   ∴Ms
3. Hs⊃Ms      1,U.I.
4. Ms          3,2, M.P.

全称概括原则 U.G.

从一个命题函项关于任意选取的个体名称的代入例，我们可以有效的推出该命题函项的全称量化式、这个规则允许我们进行概括，也就是从一个特定的代入例进到一个概括的或全称量化的表达式，称为全称概括原则，简写为“U.G.”

y 指称“任意选取的个体”

1 2	U.G.: Φy ∴(x)(Φx)

存在列举原则 E.I.

从一个命题函项的存在量化式，可以推得关于在其语境中早先没有出现过的任一个体常元（除y外）的代入例，这个推论规则叫做存在列举原则，可缩写为“E.I.”

1 2	E.I.: (∃x)(Φx) ∴Φν [ν 是任一在语境中先前没有出现过的个体常元(除y外)]

E.I. 的限制，只能含有一个在语境中早先没出现过的个体符号(除y之外)，为避免这种错误，在任何要使用E.I.和U.I.的证明中，应该总是先使用E.I.

存在概括原则 E.G.

从一个命题函项的任一为真的代入例，我们可以有效的推出该命题函项的存在量化式，这个推论规则叫存在概括原则，缩写为“E.G.”

1 2	E.G.: Φν [ν 是任一个体符号] ∴(∃x)(Φx)

例子：

1
2
3

所有罪犯都是邪恶的。
有些人是罪犯。
因此有些人都是邪恶的。

符号化：

1
2
3

(x)(Cx⊃Vx)
(∃x)(Hx·Cx)
∴(∃x)(Hx·Vx)

证明：

1. (x)(Cx⊃Vx)
2. (∃x)(Hx·Cx)
   ∴(∃x)(Hx·Vx)
3. Ha·Ca            2,E.I.
4. Ca⊃Va            1,U.I.
5. Ca·Ha            3,Com.
6. Ca               5,Simp.
7. Va               4,6,M.P.
8. Ha               3,Simp.
9. Ha·Va            8,7,Conj.
10. (∃x)(Hx·Vx)     9,E.G.

无效性证明

证明一个含有普遍命题的论证无效的程序如下：

首先考察一个只有一个个体 a 的一元模型。
写出该论证相对于此模型的逻辑等价真值函项论证。
把原论证的每个普遍命题转化为该命题函项关于a的代入例，进行真值指派就可以证明该真值函项的论证无效。如果做不到这一点，就接着考察一个含有两个个体a和b的二元模型。将a和b用合取结合起来。

非三段论推论

在对更复杂的命题函项而产生的普遍命题进行符号化时，必须小心不要被日常语言的表述方式所误导。我们不能依照任何形式的或机械的规则来把自然语言翻译成逻辑符号。在每种情形下，必须理解自然语言语句的意义，然后用命题函项和量词术语加以符号化。

除外命题：

除以前的获胜者外，都符合条件。也可以翻译为当且仅当这个人不是以前的获胜者才符合条件。

符号化： (x)(Px⊃~Ex)·(~Px⊃Ex) 也可以符号化为 (x)(Ex≡~Px)

归纳

论证基于被相信或者假定为真的前提之上，但是我们必须依靠的大量前提不能通过演绎来确立。要确立实际的事情我们必须依靠归纳（inductive）推理。归纳可以确立实际的事情。

演绎在我们已知的命题前进到由那些前提推导出其他命题方面是有力的，但是在最初的真理方面，演绎是不充分的。归纳是我们推理的起点或者基础。

演绎当中的结论与前提之间的关系是一种逻辑必然(logical necessity). 归纳论证不是这种关系，归纳的领域中，没有什么东西是确定无疑的，前提对结论的支持是或然（probable）。

类比论证

类比是从过去经验到未来去向的我们日常推理的共同点。(这家馆子的土豆丝味道不错，那烧茄子豆角味道也应该很好吃)

一些人认为教师资格测验是不公正的双重测试。
“教师已经是大学毕业生，”他们说，“他们为什么还要被测试？”
那这很简单。律师是大学毕业生，而且还是专业学院的毕业生，但他们不得不参加律师资格考试。还有其他大量的行业，如会计、精算师、医生、建筑师行业，这些行业对想成为其成员的人要求参加并通过考试，以证明他们的专业素质。教师没有理由不这样做。

用判断律师和医生资格的方法可能并不适合于判断教师资格。在所有的类比论证中，尽管前提是真的，而结论为假明显是可能的，或者说是逻辑可能的。类比论证不是按照有效和无效来区分，我们只能用概率来刻画它们。

类比的非论证使用

用于使描述更为生动，隐喻和明喻可以为读者心中创造鲜活的画面。“她的笑像花一样灿烂”
用于说明，将读者可能不熟悉的东西，与读者假定更为熟悉的，与之具有一定相似之处的另一种东西进行对照。而使某种程度上更容易为读者理解。

类比的定义：在两个或更多的实体之间进行类比，就是表明它们在一个或多个方面上是类似的。

类比论证

首先断定两个事物在两个方面类似，其次断定了其中一个事物具有另外一个特点，从而推论得出另一事物也具有这个特点的结论。

a,b,c,d 是实体， P,Q,R是熟悉或方面(respects), 一个类比论证可以表示成如下形式

1
2
3

a,b,c,d 均具有属性P和Q。
a,b,c 具有属性R。
因而d可能具有属性R。

类比论证的评价

类比论证强度的6个标准

实体数量：实体数——即过去经历数——越大，论证越强。
前提中实例的多样性: 类比论证的前提中所涉及的实例越不相似，论证越强。
相似方面的数量：结论与前提类似的方面越多，结论越可靠。
相关性：当相似方面是相关的时候（如鞋子的样式，加个以及材料）相似方面便增加论证的力度，并且，单个的具有高相关因素比一批不相关的类似对论证的贡献更大。相关指的是类比物之间存在某种因果联系的时候，它们之间存在相关。因果连接是评价类比论证的关键。
差异性：差异使类比论证减弱。差异是反对类比论证的主要武器。
结论所做的断言：结论相对于前提而言是否适度。断言越适度，加与前提的负担越轻，并且论证越强，断言越大胆，前提的负担越重，论证也就减弱。

逻辑类推反驳技术

逻辑类推(logical analogy)

从逻辑观点来看，论证形式与论证内容不同，形式是论证的最重要方面。因而，我们往往通过表名另外一个被认为是错误的论证，与给定的论证有相同的逻辑形式，而证明该论证是不牢靠的。

演绎情况中对一给定论证进行反驳性类比：构建另一个无效论证，其形式与给定论证一样，但其前提是真的，结论则是假的。其论证是无效的，因而遭攻击的论证也是无效的。

归纳论证的情况下，我们目前所考虑的是逻辑类推的反驳技术，，它同样可以是有效的。我们攻击一个归纳论证时，我们可以提出另外一个具有同样形式的归纳论证，但是该论证明显有缺陷，因而结论十分可疑。

通过逻辑类推进行反驳的一些提示性短语：“你不如说……” 在类比性反驳明显的地方，可能不需要任何提示性语言。

当反驳性论证与目标论证之间有十分重要的差异，而这些差异倾向于强化受攻击的那个论证，那么粗心的试图用类比来反驳一个论证就会适得其反。

因果推理

在我们做出行动并且试图达到某种结果的任何领域里，因果关系都是基本的。如果原因和结果之间的假定关系是被正确地建立起来的，那么基于那些关系的推理就是十分强有力的。

原因的三种含义：

必要条件：在缺乏它的情况下，该事件不能发生。
充分条件：它出现的情况下事件必定发生。
关键因素：在特定结果的产生中扮演起因的角色。

一个事件的发生可能有多个必要条件，并且所有这些必要条件必定包含在那个事件的充分条件里。

原因的意义有时是必要条件(在需要排除一些不合意的现象时使用)，普遍是作为充分条件(产生某个合意的现象)使用。我们必须清楚所使用的到底是那些意义中的哪一个。

当存在一个因果序列——时间的链条时，原因还可以细分为：最近(proximate)的原因——在事件链条中离它最近的事件，其他是遥远(remote)的原因。

原因在不同意上的区分：

仅当在原因的必要条件含义上，我们才能合法的从结果推出原因。
仅当在原因的充分条件含义上，我们才能从原因推出结果。
但推论既从原因到结果，又从结果到原因时，“原因”这个词必定是在充分且必要的意义上使用的。

因果律和自然的齐一性

“原因” 的每一种用法都预设了：原因和结果齐一地(uniformly)相连。我们承认某个特定的事态是某个特定结果的原因，仅当我们承认类似的原因产生类似的结果。

当我们使用“原因”这个词时，其部分意义是，产生某个结果的一个原因，其每一次出现都是普遍因果律——如此事态总是伴随着如此现象——的一个实例或事例

断定一个特定事态是一个特定现象的原因意味着存在某种因果律，每一个关于因果连接的断定包含了普遍性这一关键要素。

因果律——当我们使用该术语的时候——断定一个事态恒常地伴随着一个特定种类的现象，而无论该事态发生于何时何地。

因果关系不是纯粹逻辑的或纯粹演绎的。正如休谟所强调的，它不能被任何先验的推理所发现。因果律只能经验的或后验地(即诉诸经验)发现。

我们的经验总是与特定事态，特定现象以及它们的特定次序有关。我们观察到的一个事态C，并且我们观察到的可能伴随着一个现象P。我们如何建立一个普遍的因果关系，如何在我们经历的,普遍的命题特例中，得到C的所有情况下都伴随有P? 在说C引起P的时候就包含了这样的问题。

简单枚举归纳法

从特定经验事实中得到普遍命题的过程称作归纳概括。

简单枚举归纳法形式：

现象E的实例 1 伴随有事态C。
现象E的实例 2 伴随有事态C。
现象E的实例 3 伴随有事态C。
—————————————————————————————————
因而，现象 E 的每个实例都版所有事态 C

简单枚举归纳法类似于类比论证，所不同的是它形成的结论更为普遍。当一个现象的若干实例恒常地伴随有一特定类型的事态的时候，我们很自然的得出它们之间存在一个因果关系。

简单枚举法论证和类比论证非常类似，类似的评价标准也同样适用于它们。伴随着事态C的现象E的不同实例或场合，往往被称作断定C引起E的因果律的确证实例。

简单枚举归纳的缺陷：

简单枚举法对提出的因果律的例外情况没有解释。任何断言的因果律都会被一个否定性的情况所推翻。例外反证(disprove)了该规则.

如果将自己局限于简单枚举论证，就会产生一个严重的缺陷。我们将不会去注意哪些否定性的实例。尽管简单枚举规则法提出的因果律很有价值，但它根本不适合检验因果律。

因果分析的方法 (密尔五法)

被称为密尔(穆勒)方法 Mill’s methods 的归纳推理的五种技术：

求同法(The Method of Agreement)
求异法(The Method of Difference)
求同求异并用法(The Joint Method of Agreement and Difference)
剩余法(The Method of Residues)
共变法(The Method of Concomitant Variation)

求同法

被研究现象出现的若干个场合中，仅有一个共同的情况，那么这个共同的情况是被研究现象的原因(或结果)

求同法示意图（大写字母表示事态，小写字母代表现象）：

A,B,C,D 与 w,x,y,z 一起发生。
A,E,F,G 与 w,t,u,v 一起发生。
————————————————————————————
因此, A 是 w 的原因。

求同法的局限性：

很难收集可用数据，以使得确定特定现象所有实例的共同事态。
当研究显示所有情况的共同事态不止一个时，就无法对选择进行评价了。

求同法是根据部分场合中所显示的关系来推论两现象间的因果联系，而且是以相关场合中有一个共同情况为基础的，因此，其前提与结论之间的联系不具有必然性。

求同法的特点是：异中求同。

求异法

在被研究对象出现地场合现象发生了，在另外一个与前一个场合其他条件都相同场合中被研究对象没有出现，现象没有发生。那么该现象就是被研究对象地原因或必不可少地部分原因。

A,B,C,D 与 w,x,y,z 一起发生。
B,C,D 与 x,y,z 一起发生
————————————————————————
因此，A 是 w 的原因或结果，或w的原因中一个不可或缺的部分。

求同求异并用法

求同法和求异法可以同时用来对结论的支持，在许多科学研究中，这种联合运用的成为威力极强的归纳推理模式。

如果在被研究现象a出现的各个场合中，都有一个共同情况A，而在被研究现象a不出现的各个场合，都没有这个共同情况A，那么这个情况A与被研究现象a之间就有因果联系。

剩余法

从一个现象中去除部分事件已知的原因和结果，那么该现象的剩余的部分便是剩余前件的结果。

A,B,C —— x,y,z
已知 B 是 y 的原因
已知 C 是 z 的原因
————————————————————
因此 A 是 x 的原因

剩余法能够仅通过对一个事例的考察而得以使用，其他方法需要考察至少两个事例，并且，剩余法似乎依赖于预先建立的因果律。其他方法则不是。剩余法是归纳法，而非演绎法，因为它产生的结论是或然的，而不能从他们的前提中有效地演绎出来。

共变法

以上四种方法本质上都是排除性的。通过排除一个给定现象的某些可能原因，从而对某些假定的因果解释提供支持。这些方法在经济学，物理学，医学，以及在一个因素大体上的增或减的任何地方，完全排除任何一个因素都是不可行的。

在其他条件不变的情况下，如果某一现象发生变化另一现象也随之发生相应变化，那么，前一现象或是后一现象的原因。

① A1BC a1
② A2BC a2
③ A3BC a3
… … …
所以 A是a的原因

归纳技术的局限

密尔五法中假定人们可以确定“仅有一个事态相同”的场合或者“除了一个事态其余的每个事态都相同”的其他场合。事实上不存在两个事物可以只在一个方面不同，我们甚至也不可能检查所有可能的事态。因此这些方法作为科学发现的工具并不充分。

归纳依赖于隐含假说的价值，表明了归纳技术本身并不能提供因果证明。

归纳方法的应用总是依赖于观察到的相关性，即使观察是十分精确的，但这样的观察也可能是不完全的，因而是欺骗性的，我们不能从那些没有被观察到的事例中确定性的推出一个因果连接。

这些局限性再一次说明了归纳和演绎之间的鸿沟。一个有效演绎推理构成一个证明。但是每一个归纳推理充其量是高度可能的(probable)，决不能成为结论的。因而，密尔关于他的准则是“证明的方法”，“发现的方法之全部”的声称，都必须被拒绝。

由于研究者不可能将所有的事态都考虑进去，必须总是假定关于被考察事态的因果假说，但不确定哪些因素是被考察现象的原因时，我们经常构想出替代性的多个假说，并让每一个假说接受检测。本质上主要是排除性的这些归纳方法所能让我们确定的是：如果对先行事态的某个特定分析是正确的，那么这些因素中的一个因素不可能是或必定是被研究对象的原因（或部分原因)。这可能是演绎出来的，并且这个演绎可能是有效地，但是哪个论证的可靠性将总是取决于已假定的先行分析的正确性。

这些方法不是发现的通路，也不是证明的规则。它们是检验假说的工具。这些归纳技术的主张合起来描述了对照实验的普遍方法，这是在所有现代科学中的一个普遍和不可缺少的工具。

科学与概率

科学和假说

科学说明

科学的目标就是发现普遍真理，据此我们所遭遇的事实可以得到说明(explained)

一个好的说明必须提供与待说明的事实相关的(relevant)真理。

一个科学理论所能解释的事实越多，它的力度就越强。

科学和非科学说明的区别：

态度上的区别：
- 一个非科学的说明是被教条的提出的；它给出的解释被认为是绝对真的而不能改进。
- 一个严肃的科学家态度是非教条的；每个提出的说明都是暂时的或临时的；
- 假说可能被认为很有可能是真的，但是它们被视为会在证据面前被替换。
- 科学中所有普遍命题在本质上都是假说，永远不具有绝对的确定性。
解释所基于的基础
- 科学的假说仅仅在存在好的证据条件下才值得接受。
- 一个非科学信念被坚持，可能不依赖于证据。
- 一个非科学的说明被简单地认为是真的，可能是因为“每个人知道”它如此，或者可能是因为是由上天所揭示的。这样的断言没有可靠的检验。
- 真正的科学中，对于真理的断言可以得到检验，并且这样的检验在于经验之中，因而我们说真正的科学是经验的。
- 非科学假说，不能够从中演绎出其他的可直接检验的命题
- 一个给定现象的任何一个科学说明能够演绎出可直接检验的命题，而不是陈述待说明事实的命题。这就是一个说明是经验可证实所表达的意思。

假说和确证

研究科学的7个步骤

确定问题
构建初步假说
收集额外事实
形成说明性的假说
推导出进一步的结果
对结果进行检验
应用该理论

对科学说明的评价

与原有完善的假说的协调性
预测力
简单性

作为假说的分类

概率

概率是全部归纳逻辑中一个核心评价性的概念。科学理论及其包括的因果律也仅仅是或然的，即最好的归纳论证也不具有有效演绎论证所拥有的那种确定性。

我们为理论指派概率，这种概率的表达式推论得到的。

区分概率在使用中的两种附加含义：

A. 概率的先验解释。

“抛硬币正面朝上的概率是1/2”

一个事件的概率的断定是根据人们合理地相信那个事件将发生的程度。称之为概率的先验理论。

B. 概率的相对频率解释。

“16-35岁女性的驾驶员的事故率是0.324”

一个事件的概率依赖于这个事件发生的相对频率。这里的概率被定义成体现一个特定属性的一个类的成员的相对频率

概率的计算

乘法定理

共同发生的概率

两个独立事件共同发生的概率等于它们各自概率的乘积 (乘法定理)

P(a·b)=P(a)xP(b)

乘法定理一般化，任意多个独立事件的共同发生的概率等于他们各自概率的乘积

加法定理

计算两个或更多替代性发生的时间的概率方法。

A. 两个互不相容事件的并的概率等于这两个事件的概率的和，即

P(a+b) = P(a) + P(b)

有限个互不相容事件的和的概率等于这些事件的概率的和，即

P(A1+A2+…+An) = P(A1) + P(A2) + … P(An)

如果事件A1,A2,…,An 构成互不相容的完备事件组，则这些事件的概率的和等于1，即

P(A1+A2+…An) = 1

日常生活中的概率

我们需要在教育，择业及生活中的其他方面的诸多可能性之间进行协调，有两个因素需要考虑：安全性(safety)和回报率(productivity)。他们往往不可兼得，较高的回报通常蕴藏着较大的风险。我们想知道我们在金钱或时间与精力上的投资是否“值得”；未来不可知，但能够估计其概率。

当人们要对任何“不确定(chancy)”决策进行比较时，期望值概念是一个好用的工具。我们将每个可能结果下产生的收益与实现该结果的概率值相乘，这些乘积之和，即为赌博或投资的期望值。

抛硬币期望值计算：打1块钱赌，一赔一赌硬币正面朝上。

获得2块钱(其中1块钱是成本)的几率是1/2 或的0元的几率是 1/2

该赌博的期望值是：(1/2 x 2)+(1/2 x 0) 该值为 1 块钱。所以机会是均等的。

下一次投掷一枚公平的硬币时出现正面（或反面）的概率不会受前面的投掷结果影响，每一次投掷都是独立的事件。某人假定由于先前独立事件发生的频率，使得某些未来事件变得更可能发生，或更不可能发生。这样他就犯了 赌徒谬误(the gambler’s fallacy) 的大错.

If you like this blog or find it useful for you, you are welcome to comment on it. You are also welcome to share this blog, so that more people can participate in it. If the images used in the blog infringe your copyright, please contact the author to delete them. Thank you !